TRACERY

or

GOING ROUND IN CYCLES

Gavin Wraith

2009

Suppose we have a finite collection of things and a function that transforms things. Here is a picture, Fig. 1, in which the collection is a blue bag, the things are little points and the transformation is depicted by arrows. Each point has just one arrow starting from it that leads to a point. So we can think of the transformation as a journey along an arrow. If we start from a particular point and keep following arrows, I think you will agree that we must end up going round in a cycle. If the collection were infinite this would not necessarily be the case: think of the positive integers and the function that simply adds 1 to each number.

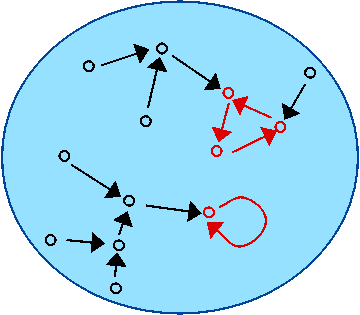
Fig. 1

In Fig.1 the cycles are shown in red. We have one 3-cycle and one 1-cycle, and a forest of hairy bits shown in black. A fixed-point of a transformation is simply a 1-cycle. Every transformation of a finite set can be thought of as a collection of cycles, each of its own size, together with a collection of trees (hairy bits) rooted at some of the points of the cycles. If the transformation is invertible, i.e. a permutation, then there are no hairy bits, just cycles. We use the notation for an n-cycle. So we can say that the cycle-pattern, or trace, of the transformation depicted in Fig.1 is . A transformation with 7 fixed points and 2 100-cycles would have trace and so on.

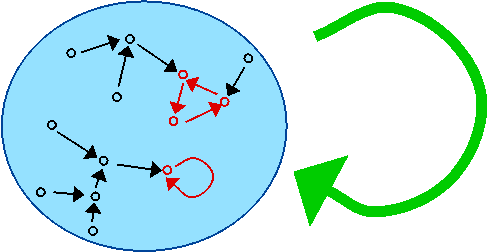
Fig. 2

Fig. 2 shows the same transformation as Fig. 1 but this time we have drawn a big green arrow going from the blue bag to itself, depicting the transformation. The actual effect of the transformation is shown by the black and red arrows inside the blue bag. The green arrow goes from bags to bags, not points to points - it lives on a higher categorical plane!

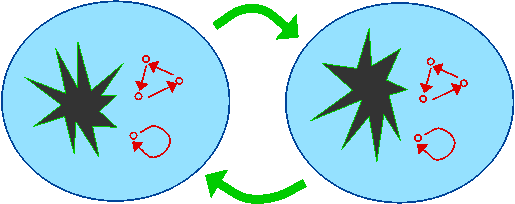
Fig. 3

Now let us suppose we have two finite bags, depicted in Fig. 3 at the left and at the right. We will call them and , respectively. Suppose also that we have two functions, each depicted by a green arrow, going from the left bag to the right bag, and from the right bag to the left bag. In other words

By following round the arrows we get two transformations: and .

Here is the surprising fact: the two transformations have the same trace. That is

You might like to draw your own pictures to prove why this is so.

Furthermore, this property of the trace is characteristic. In other words, any property that cannot distinguish between the two transformations we get when we compose functions going in opposite directions between two finite sets, has to depend purely on the trace of a transformation. Put another way: the property cannot depend on the hairy bits. That is why the hairy bits have been left undrawn in Fig. 3.

We can add transformations. We just stick bags together. The trace of a sum is quite evidently the sum of the traces. Every transformation can be written as a sum of monocyclic ones (that have just one cycle each).

But we can also multiply transformations. If we have

then we have

given by . How do we multiply cycles? If and denote highest common factor and least common multiple, then

With this rule, trace preserves multiplication.

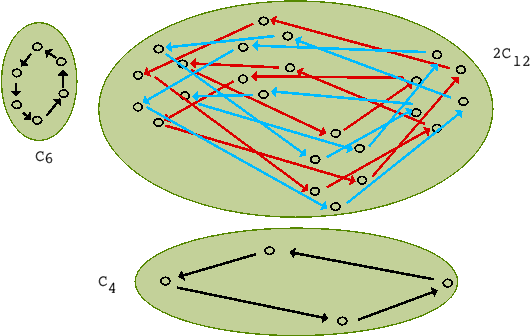
Fig. 4

In Fig. 4 we see the case and . The product consists of two 12-cycles, shown in red and blue. Every cycle can be written uniquely as a product of cycles of distinct prime-power size. If we factorize an integer into a product of distinct prime-powers:

then

So we can factorize as . Note that , and that is irreducible, i.e. cannot be factored.

Postscript for the numerate

Those who know some linear algebra may already have met the word trace and may be wondering if there is a connection. We can replace finite set by finite-dimensional vectorspace (over some fixed ground field of scalars), and transformation by -linear transformation, and function by -linear map. Then the trace of a -linear transformation is now the element of got by adding up all the diagonal elements of a matrix representing it. Again, the property

is characteristic. Furthermore, if we add and multiply -linear transformations using the operations of direct sum () and tensorproduct () then trace preserves addition and multiplication.

Postscript for the category theorist

The trace of a category is the coend of its Hom functor. That is to say it is the collection of all maps from objects to themselves modulo the relation generated by identifying and whenever and are maps of in opposite directions. The notion of trace can be extended to any functor and this notion is itself a trace on the bicategory of categories and profunctors. So we are not so much going round in circles as spiralling up a ladder. This explains why the trace often tends to have, and preserve, algebraic structure.

So we have seen that the trace of the category of finite sets and functions is the same as that of the subcategory of finite sets and bijections, and has a rig-structure. The rig has an additive basis given by the for , and multiplication given by the formula above. In fact it has more: it has a -rig structure. The category of finite sets and bijections has endofunctors for which assign to a set the set of its -element subsets. Note that this functor does not lift to the whole category of finite sets and functions.